Wartajateng.id – Dalam matematika ada salah satu materi yang cukup ditakuti oleh semua orang. Materi itu adalah trigonometri yang cukup rumit karena memiliki banyak sekali rumus dan juga perbandingan. Apalagi tabel trigonometri cukup sulit untuk dihafalkan bagi beberapa orang.
Pada pembahasan ini kamu akan mengetahui beberapa tabel trigonometri yang berhubungan dengan sudut khusus. Sudut ini biasanya cukup mudah dihafalkan. Selain itu nilainya juga tidak dalam bentuk pecahan yang sangat rumit.
Untuk mengetahui seperti apa trigonometri dan beberapa tabel hasil nilai yang diberikan. Ada baiknya untuk menyimak beberapa alasan yang akan dibahas di bawah ini. Dengan begitu kamu bisa langsung mengetahui seperti apa nilai dari sudut dalam segitiga atau bangunan geometri lainnya.
Mengenal Trigonometri

Trigonometri adalah salah satu cabang dari matematika yang membahas hubungan antara panjang suatu sisi segitiga dengan sudut yang ada di belakangnya. Hubungan ini sangat jelas sehingga dengan hanya melihat panjang sisi sudut bisa diketahui begitupun sebaliknya.
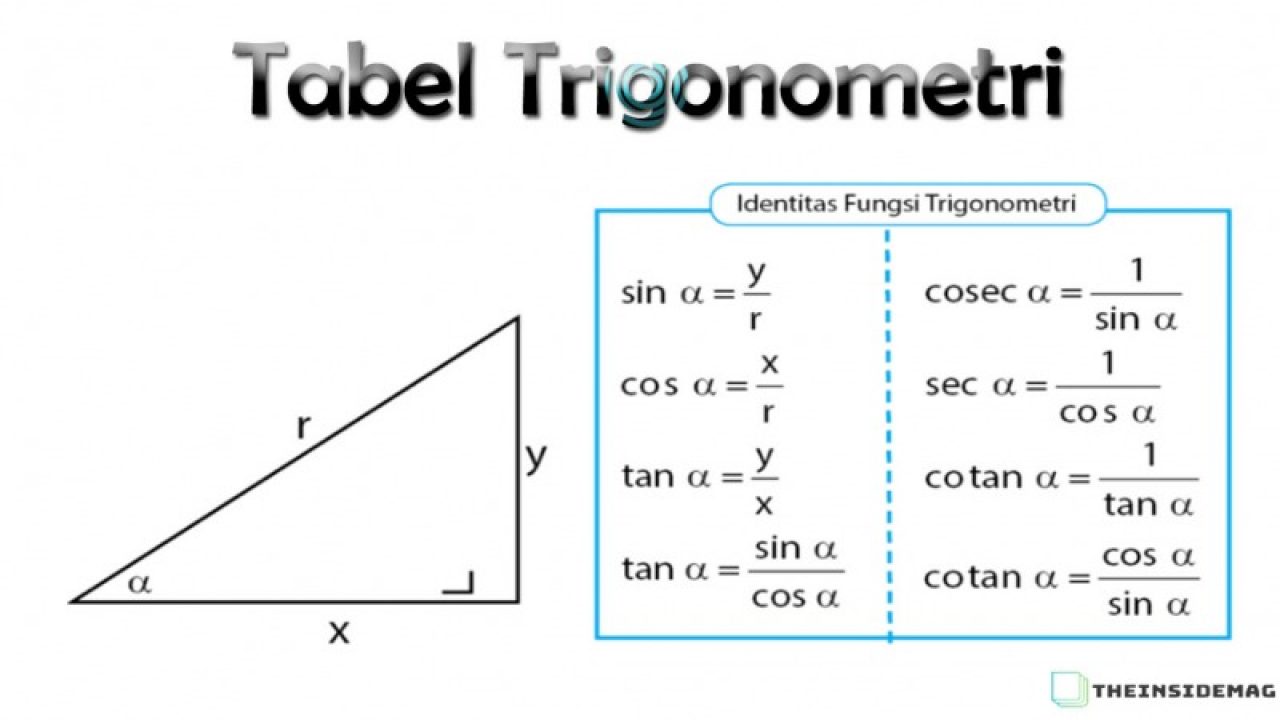
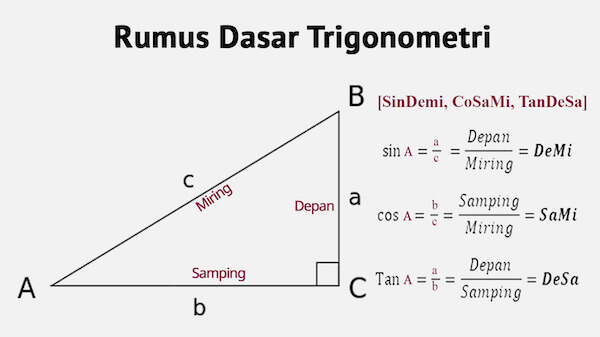
Karena memiliki hubungan maka ada beberapa korelasi antara masing-masing sisi dan sudut. Bandingan antara sisi tertentu akan menghasilkan suatu hal bernama Sin atau sinus, Cos, dan Tan atau tangen.
Ketiga trio trigonometri ini merupakan perbandingan dari beberapa sisi yang ada di dalam segitiga.
- Sin, merupakan perbandingan antara sisi depan dan sisi miring. Maksud dari depan ini adalah sisi yang ada di depan dari sudut.
- Cos, merupakan perbandingan antara sisi sebelah samping dan sisi miring.
- Tan, merupakan perbandingan sisi yang berada di depan dari sudut apel sisi depan dibagi sisi samping.
Perbandingan ini bisa digunakan untuk berbagai hal seperti penghitungan tinggi suatu bangunan hingga beberapa perhitungan lainnya. Artinya perbandingan sudut dan sisi ini sudah tidak bisa diubah-ubah karena sudah memiliki pakem tersendiri.
Itulah kenapa nilai dari Sin, Cos, dan Tan biasanya memiliki persamaan bahkan pada nilai-nilai tertentu. Untuk memudahkan mengetahui biasanya akan ada tabel tertentu untuk sudut khusus atau untuk semua sudut mulai dari nol derajat hingga 90 derajat.
Nilai Trigonometri Berdasar Kuadran
Nilai trigonometri biasanya berbeda-beda antara sudut yang ada di kuadran pertama dan sudut yang ada di 3 kuadran selanjutnya. Dalam satu bidang akan ada 4 kuadrat yang masing-masing kuadran merupakan kelipatan dari 90.
1. Kuadran I
Kuadran pertama berada pada nilai nol hingga 90 derajat. Semua nilai sin cos tan yang ada di kuadran ini adalah positif.
2. Kuadran II
Pada kuadran kedua ini dimulai dari 90 derajat hingga 180 derajat. Pada nilai ini yang memiliki nilai positif hanya sinus.